"All models are wrong, but some are useful."

-George Box

Note: this is part 1, laying out some theory, abstraction, and algebra for later posts on content (part 2) and interfaces (part 3). You can read them without reading this, but it might help.

Aphorisms

I'm not opposed to "x's law" as a shorthand for a particular type of common sense. I've actually been quite enthusiastic about them in the past. They are useful for jargon, in-jokes, and occasionally to make a valid point.

But they can also reflect an undue reproduction and reverence of old values, and serve to short-circuit interrogation.

Any classic text or phrase can be used similarly. Maybe this is why so much effort seems to be focused on that which is ephemeral, incomprehensible except in the moment. When subversive structural critique can only do so much, shitposting at least guarantees its only legacy is simultaneously vacuous while still taking up space.

In any case, aphorisms are an easier mark than dogma, legalese or society in general, because they are less broadly applied yet contextually potent. As with company values or mission statements, aphorisms give minimodels – wrong but useful.

The Models We Use In Software

In addition to more general sayings or "bits of wisdom" or whatever, we also have the historical baggage of a broken math education and a ludicrous skepticism of "non-stem fields."

We're also quite heavily optimized for, oddly enough, either CS first year/analytic geometry (the combination of these is basically Big O notation) or sufficiently more math-heavy positions. In programming as I've experienced it, we're leaving the best math on the table, and what we do is mostly model processes and relationships.

In many cases, our tools match our abstractions to accomplish this goal. In other words, the name of the method we use or SQL syntax are the same as our mental model of what is happening. In the sense that this eliminates our need to care about implementation details, this is great. In some cases, given a new package that resembles the one we know well, we may be able to easily translate one to the other. And when things don't line up so well, if we know the more general names (maybe these are the "math words") for the parts of the tools, this process might be easier.

In the worst case scenario, tool changes are catastrophic. We might not know the general terms or potentially, the model of a tool is highly specialized and difficult to abstract.

I'd suggest that the best features we encounter and create so frequently are not so unique, and a little bit of math can help us more than learning every framework (or other tooling) variation.

This math is (for unpleasant reasons and terrible effect) locked behind years of calculus, despite it being quite accessible, especially to working programmers.

As a result of where it (and by "it" I mean "abstract algebra") sits (early to mid college level), it's trapped in 3 ways. First, the vast majority of students don't get to it. They take the math that they must and endure the humiliation and drudgery only as long as they have to. Assuming a non-stem major, they'll probably cut out early into calculus or maybe an applied course involving statistics. Some stem students will be in a similar position, only taking what is requisite to their major (which is unlikely to include this topic). Second, for the more advanced math student, this course sits late enough that it carries all the weight of previous courses. They (and teachers with this experience) have a ton of other stuff in their heads, and might not see the value (including their applications) of these topics to people without the same background. Last, they may be onto other topics and career paths (of a less "applied" variety) very quickly, where these topics are less important.

Shallow Math

What I'm suggesting would be controversial in a field insisting on a more rigorous approach. Specifically, we should snag the good stuff we can, even ill-formed or without the depth in the topic. If we're fine with tools providing us with abstractions, making up our own, or using aphorisms and trends to guide us, we might as well borrow from here too.

It bears reiterating at this point that these models may not be "right" in the sense that they fit the mathematical idea perfectly, but it seems like a decent enough thing to try.

By the way, there is a bit of a very short motivating text here by Gilbert Strand that suggests something as transformative but less radical (Strang advocates teaching linear algebra before calculus). I'm suggesting we could bring abstract algebra in even earlier with a linear algebra capstone (in addition to relaxing the rigor mostly by letting go of the reified forms that take so much set up... (like Strand, I mean calculus here)).

This is not to say that the math presented in this article is easy. It's worse than that. It's simultaneously trivial for anyone deep into mathematics, and hard for the uninterested (which is completely understandable given that mathematical curiosity gets beaten out of most in a terrible high school experience).

But if there was one math topic beyond arithmetic that I would advocate be part of our education, modeling systems like this would preempt calculus, statistics, trigonometry, geometry, and even a comparatively deep study in numerical algebra that a high school education exposes us to. On a professional level, this is useful not just for traditional engineers, programmers, and designers, but also for systems-thinking in journalism, law, art, and basically any other career I can imagine.

Moreover, patterns like these, the expectations they create, are bound to come up, even if accidentally, in our daily lives. "Program or be programmed" is an individualist call to sink or swim. "Shallow math should be common sense" can't escape a similar criticism, but for two distinctions. First, by the end of this article, I hope to introduce a formal basis for use in critiquing extant systems. Second, for software engineers and designers, perhaps this can inspire a more considerate approach. A tentative third, purely fantastical, would be this being of general interest and concern. Everyone learning to program as an individual pursuit of power, with few exceptions, reinforces a quasi-caste system. Everyone having a shared ability to abstract and reason about how power, attention, and information move would be revolutionary.

The Models We Can Have

So anyways, we can take a look at a few mathematical objects and see how they might help our modeling abilities.

Functions

When they resemble mathematical functions (meaning they have only explicit inputs, a return value, and no "side-effects"), they model implication. In other words, "if input(s), then output." Even if the types of inputs/outputs aren't explicitly stated, they should be knowable.

When run by tests or live, these model a direct proof of a system. An error message (if formatted as "if not q, then not p") provides a prompt for the beginning of a contrapositive proof.

When characterization tests are used ("if inputs, then wrong output"), we have the basis for a proof by contradiction when the test runner reports the departure from truth.

From a feature perspective, functions are the foundation of a working system. If this happens, then this happens, then this happens, etc. If there's a bad path, you have functions that don't fit together (they don't compose).

Functors (map) f a -> f b

Functions might have any type as input or output. Functors have a "fluent interface," (with the map function) meaning the input type and output type match. The most common example of a functor is an array. Map takes an array as input and returns an array.

A lot of functional programming works toward this end. Fluent interfaces are essentially "closure," a mathematical property that aids in composing the same thing together.

Functors give an interface that cycles back on itself (you can call map on an output of map), but allows its inner part to change. Monads expand the variety of composition that is possible. There's a ton of variation here, but the two main properties of concern are composition and identity.

From a feature perspective, "composition" lets you do the same operation (eg. an array's map) as much as you want. "Identity" gives you a "no-op" that doesn't change anything. Consider a saving function of an online editor. Saving an already saved document should look like a no-op (even if in the background it might update a timestamp). Implementation-wise, a lot of complexity in software comes from the special cases around no-ops (null, empty arrays, etc.). Elegantly handling these means using a monad, a more flexible structure than functors.

Sum and Product

The alternative to using a monad is an "if statement." In FP terms, this structure and others like it are generalized by the concept of "sum." There is also a corresponding notion of "product."

This is a bit abstract, but to see how these relate, we can use functions as a good example. Here is this notion in JavaScript as a sum:

f = (param) => {
  if (param == a){
    // some output
  } else { // if param is b
    // some output
  }
}

The possible output values will be additive. The a cases plus the b cases.

As for product:

f(a, b) = // some output using a with b

The possible output values are bounded by the number of possible a's times the number of possible b's.

From a feature perspective, creating a sum is enabling a choice. Creating a product is enabling some combination of values to exist. The common notion of algebra of sums and products (including distributivity where a*b + a*c = a(b+c))  applies to this system as well. Without more limit-inducing structures in place, the number of possibilities in programs and interfaces is gigantic and unpredictable.

Also from a feature perspective, the product can inform a "unix philosophy" of tools that combine together or of API access that allows interesting mixes of data. A band releasing individual tracks is a non-"tech" example.  

(by the way, functions/implications themselves create an exponential possibility f(a) = b, b^a if you're interested in an algebra of implementations as well as of test cases)

Groups, Commutative Groups

The identity is key to functors and monads (it introduces a "no-op," remember?), but groups inspire a bit more, feature-wise.

But before we get to that, we need a few mathy bits. The integers, -infinity through infinity under addition are a group. Tautologically, this means that they adhere to the definition of a group. Let's have letters like "a" mean any number in that set -infinity through infinity.

a + 0 = a (identity)

a + -a = 0 (inverse)

a + b = c | a, b, c are all members of the group (closure)

(a + b) + c = a + (b + c) (associativity)

From a feature perspective, we've talked about identity before as no-ops, but the inverse is an undo feature. Reverting a git commit. Unapplying a photoshop filter. Deployment rollbacks. An inverse is what allows you to traverse a timeline backwards.

Closure is what defines an operation can happen with any member of the group (and ensures a fluent interface like map has). The inflection points, where objects change in a system and become something else are particularly vulnerable to confused programming and interfaces. Back to the editor example, if I start with a "document," and saving it changes it to a "saved document," then I need an abstraction to treat things differently. Adhering, when possible to this notion closure of a group with, for example, interface-editable objects (eg. custom forms) may inform better implementations and interfaces.

Associativity is a bit complicated because it doesn't have a great interpretation in terms of sequential actions, so a feature-level description for an individual interacting with an interface is difficult. In general, associativity will be good to keep in mind if you have some "divide-and-conquer" feature in mind. If you are creating processes with queries and filters, considering associativity may be beneficial. From the backend side of things, concurrent systems benefit from associativity by allowing options for partitioning.

However, if we want to admit those pieces in arbitrary order, we'll need commutativity. When we add commutativity to a group, we get a "commutative group," also called an "abelian group." Commutativity is vital and a lack of it is a source of serious confusion and difficulty. For instance (again from a feature perspective), if someone signs up to a website with an email address and later links an oauth provider, their account should be quite similar (to them in the interface and programmers on the backend) as if they had signed up through an oauth provider and added an email address to their profile later on.

Lattices

All of the structures discussed so far have been responsible for better interfaces and implementations. It seems that the more of the properties above are included (even if not considered from this perspective), the richer and more secure an interface can be. But whereas to these structures give rise to safe, featureful, reasonable programs, lattices generalize structures of commonality, truth, and importance.

The definition of a lattice is a bit more complicated as compared with earlier objects, so there will be a bit more setup before we can introduce the feature perspective. A lattice involves two operations (meet and join), and has our familiar properties of commutativity and associativity. But adds two more: absorption and idempotence.

Idempotence means that applying the same operation any number of times will yield the same result. The identity (like adding by 0) is idempotent. Calling toString on an array in js is idempotent. ([1, 2].toString() =  [1, 2].toString().toString()).

The easiest way to understand absorption is by looking at numbers (let's say any numbers and ignore whether they are "closed" or not) under multiplication. In multiplying numbers, 0 is an "absorbing element," because the result of multiplying 0 and anything else equals 0.

We'll meet the join and join the meet in the context of particular lattice-like structures: Boolean Algebra, Total Orders, and Lattices.

Boolean Algebra

A good first application of meet and join are the familiar boolean logical operators and (∧), and or (∨). In an "or" (∨) operation, true is an absorbing element, because "a ∨ true" will always produce a true, no matter how many terms you have:

true ∨ a ∨ b ∨ c...

Similarly, a false is the absorbing element of a meet, and no matter how many terms there are, one bad apple spoils the whole bunch*:

false ∧ a ∧ b ∧ c...

Total Order

Some collections of objects can be put into a line, where each element is greater than, less than, or equal to each other. A common version of this is the number line. While we tend to use less than (<) or greater than (>) around this topic, we also do things like this a lot:

x >= y ? x : y;

or more generally:

myArray.sort()[-1];

In both cases, we're concerned with the biggest value, first as compared with just one other value, and then as the maximum of a collection (which itself relies on a comparator like in the first case. As you might suspect, we can flip these both around to get a minimum:

x <= y ? x : y;
myArray.sort()[0];

If we had the ability use these symbols in JS, we might write the comparators as functions like this:

∨ = (x, y) => x >= y ? x : y // join
∧ = (x, y) => x <= y ? x : y // meet

For a total order of numbers, the join operator returns the larger number, and the meet operator returns the smaller number.

But, let's not forget our absorbing elements, which are infinity for the join and negative infinity for the meet. More generally, these absorbing elements are also called "top" and "bottom."

Not so coincidentally, top and bottom are sometimes symbolized as ⊤ and ⊥. So that means that we can describe the absorbing elements top and bottom like this:

∨(a, ⊤) // => ⊤
∧(a, ⊥) // => ⊥

To express that as equations rather than function calls:

a ∨ ⊤ = ⊤
a ∧ ⊥ = ⊥

You might notice that ⊤ looks a lot like a capital "T." Interestingly enough, if we consider that to mean "true" and ⊥ to be "false," we can see how our boolean algebra interpretation of ∨ as "or" and ∧ as "and" works for that as well.

Lattices as Sets

The last form of lattice-like structures to examine before we get to the applications are the lattices. These can represent factorized integers as well as set inclusion. It's a bit hard to imagine them, so when considering these structures, we can use what's called a "Hasse Diagram" to get an idea of how they work. Here is one for the elements of the set {x, y, z}:

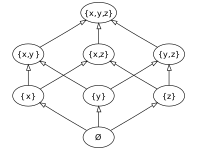
The absorbing element of the meet of this set (aka. "bottom" or ⊥) is ø, the empty set. If you meet anything with it, you'll get it back. As you might expect, the absorbing element of the join of this set (aka. "top" or ⊤) is {x, y, z}, the full set. If you join anything with it, you'll get it back.

This is a partially ordered set (not a lattice) because not all elements can be compared with one another directly. As an example, "is {z} < {x}?" doesn't have a good answer. However, their meet is ø. Also, {x, z} and {y,z} can't be compared, but their join is {x, y, z}.

Though we can't compare {x} to {y, z}, we can still regard the meet of them as ø and the join of them as {x, y, z}. In perhaps more familiar set-theoretic terms, these correspond to the intersection and union. Again, not just coincidentally, we can see a similarity in the notation:

a ∪ b (union)
a ∨ b (join/or)

a ∩ b (intersection)
a ∧ b (meet/and)

By the way, if we have a top and bottom element (⊤ and ⊥), then we can express ideas of absorption and identity as follows:

absorption
a ∪ ⊤ = ⊤ (set of all members)
a ∩ ⊥ = ⊥ (ø)

identity
a ∪ ⊥ = a
a ∩ ⊤ = a

From a feature perspective (Finally!): Lattices are everywhere: sorting, presentation, boolean logic, grouping/classification, and comparison for instance. I'd honestly say that at the "breakthrough technology or service" level, there's a lattice running the show. The google search results has a top-of-fold effect with their first result and first page. Other sites with search have followed suit.

Machine learning (roughly) enables ordering and classification.

A theory of content, and I'd argue laissez-faire economics, as a desirable "anything goes" union/join operation is a destructive fantasy. Disjoint unions (labeling content as advertising, comments, flagged content, etc.) has encumbered news organizations with extra (also necessary, messy, and expensive) work. Along the way, they've been completely destroyed by ad companies built on union for their own content, but using intersection for agreements involving money.

The "friction" of disjoint unions doesn't compare with that of intersection, which is friction of explicit agreement (arguably this doesn't apply to TOS's or other contracts where one party has much more power than another). Censorship is inherently a process of intersection, but so is consent (a ∩ ⊥ = ⊥). If our model of a social media system is to permit everything by default (a ∪ ⊤ = ⊤), then we can't be surprised when adhoc methods fail to enable safety (or just a decent experience).

So as we make choices about these kinds of features and content, (even down to the queries we execute!), we can choose when to introduce, preserve, or reduce friction. We can choose whether to, by default, keep people separate or put them together. We can decide what tools we can give people to separate themselves or come together with others.

Again from a feature perspective, lattice-like structures have the most opportunity to guide our purpose and who we serve. The alternative of just seeing what gets the most clicks is absolutely destroying us, on a personal and global scale.

But Is This Model Correct?

No. It's wrong. The complexity of human experience isn't an abstraction or an object. It's trillions of stories and theories. This is one.

But it's useful. Especially in the case of lattices. We order things. We classify things. We have limits to what we can present and standards for how to classify. We make agreements and decide when and how to include everyone.

We recreate the lattice-concepts from scratch for every argument about what kind of society we want, what is fair, and how we can get along.

Innovation would be creating a sustainable planet where we all can live (join/union). Disruption would be understanding and respecting commonalities as well as limits of participation (meet/intersection). We have a million examples** of how this plays out and decent abstractions to work with, but if our focus is on maintaining/increasing wealth for the wealthy, we'll never get around to it.

* Ripe apples produce ethylene and ripen/rot fruit around them. https://mentalfloss.com/article/31666/does-one-bad-apple-really-spoil-whole-bunch

** A few of the million examples...

One surprising anecdote I have is a case for reddit being better than twitter. On twitter, channels of content are not emphasized. If anything, the system brings conflicting groups together. Arguably, it is easier to find dedicated collaborative feeds (subreddits) of hatred on reddit, but the model of choosing streams of content is itself an intersection between what you want to see and what you can choose.  

Another way we can see the power of intersection is in DMCA takedowns. There is a strong incentive/tradition of protecting property in the US. It is stronger than protecting against negative PR (which would be censorship, although there is a consistent effort to conflate the two).

Interestingly enough, union can also be used as an operation of censorship. This is like those scenes in spy movies when a legal document is requested and a box truck brings in filing cabinets full of not so relevant information to obscure the basic facts. Zeynep Tufekci argues similarly in the context of how covering all sides (including lies) of a situation acts as censorship. And really, if lies are given even the same attention as reality (even without the man-bites-dog exceptions), the same influence, and the same interface/design (eg. tweets basically all look the same structurally), then lies absolutely win. They are cheaper to produce, and imagination is bigger than reality.

Absorbing elements are scary. Fearmongering over union/join (anything goes, ⊤, being the absorbing element) drive fear over people who aren't like us (for some vague notion of "us" and what it is like to "be" us). Fearmongering over intersection/meet (nothing, ⊥, being the absorbing element) drive fear of a consent-based, intersectional culture when you "just can't say/do anything anymore." More broadly (held by capitalists on "both sides"), if wealth doesn't obligate others to you, then what is the use of money?

I think these viewpoints are dangerous and awful, but I have my own absorbing elements to worry about. A "vicious cycle" where one outcome captures all others is an absorbing element of a markov chain. Wealth and power hording are an example of this. Outrage-driven systems like youtube recommendations are another. A planet that warms itself in part because it has already warmed itself is another.